BUAA_Object-Oriented_Unit1

三月 16, 2023

hw1

度量

Main_hw1

每个类的作用

Expr，有ArrayList<Term>，表示多个Term相加
Term，有ArrayList<Factor>表示多个Factor相乘
Factor，具有toPoly方法
Number，Factor的子类，表示带符号的数字
Var，Factor的子类，表示带幂次方的变量x或y或z
ExprFactor，Factor的子类，表示带幂次方的表达式
Poly多项式，具有ArrayList<Mono>以及若干加减和乘法的方法
Mono单项式，具有系数，x的次方数，y的次方数，z的次方数这些属性以及若干方法
Parser语法分析器，和Lexer一起使用从而把输入的String解析成一棵语法树
Lexer 词法分析器，通过next()方法来读取下一个curToken
Change对String类的字符串进行预处理

架构设计体验

由于在上学期并没有学习先导课cpp，而是选择了swift，导致hw1布置下来的时候，我对递归下降以及java 的语法完全不清楚，除了Poly和Mono还有字符串处理类之外的类我都是模仿training1进行构建的。

由于training1进行的是将表达式转化为后缀，所以我在运算表达式这一步遇到了麻烦，不知道即使将expr的结构解析出来了，又将要如何去进行复杂的运算和化简，但是这一步从往届的博客中得到了启示。

我加入了Mono类和Poly类，Mono类含有表示x的指数的indexOfX，表示y的指数的indexOfY，表示z的指数的indexOfZ，以及系数Coe，还有一个toString方法（可以进行优化以简化表达式输出）。Poly即多项式，表示许多单项式的相加。由于Number和Var可以轻易地转化为多项式和单项式，Term转化为的多项式即是其元素ArrayList中每个Factor转化为的多项式相乘，而Expr转化为的多项式即是其元素ArrayList中每个Factor转化为的多项式相加。

通过这个方法，我们把复杂的问题转化成了分割开来可以处理的小问题，降低了耦合度。单独为Mono设置单项式加减乘和为Poly设置多项式加减乘都不困难，而Expr层层调用toPoly也不困难，至于由String到Expr的解析过程则由Lexer和Parser完成。每个部分各司其职，让我初步体会到了面向对象封装、设置接口的思想的方便。

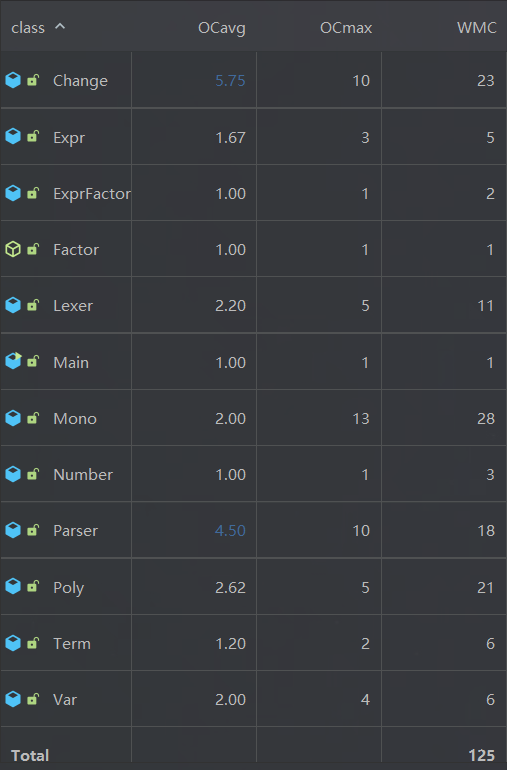
复杂度分析

OCavg是类平均圈复杂度

OCmax是类最大圈复杂度

WMC是类总圈复杂度

hw1复杂度

hw2

架构设计体验

这次作业相比hw1增加的部分是自定义函数和三角函数，因此在Factor部分新加入了SinFactor,CosFactor,FuncFactor。新加入了Define类用来记录自定义函数的名字和形式参数，也定义了方法用于替换形参和实参。在Parse部分对形式符合自定义函数的部分进行了解析。

分析bug

第一次作业和第二次作业有一个共同的bug，就是没有注意到数字是可以带符号的，在我一开始测试的一些数据里，形如“+NumFactor”的情况中，会将“+NumFactor”视作一个Term，加号会被分析为Term的符号，因此不需要解析NumFactor的符号。但是在形如“sin（Factor）”的式子里面，不考虑符号就会出现runtimeError。这是一个很简单但是却很致命的bug。

改出bug后的代码如下：

BigInteger num;
            if (lexer.peek().equals("-")) {
                lexer.next();
                num = new BigInteger("-" + lexer.peek());
            } else if (lexer.peek().equals("+")) {
                lexer.next();
                num = new BigInteger(lexer.peek());
            } else {
                num = new BigInteger(lexer.peek());//Integer.parseInt(lexer.peek());
            }
            lexer.next();
            return new Number(num);

第二次作业还有一个bug是sin和cos括号里面的内容必须是Factor，但是ExprFactor解析出来的也可能不需要加括号，而Var幂函数解析出来的反而可能要加括号，因为没有注意到这个问题，在强测中我得到了很多format error。

更改的方法是增加对字符串的判断，如果不符合Factor的定义就加上一层括号使之成为ExprFactor去符合定义，这样才能放在必须是Factor的地方。

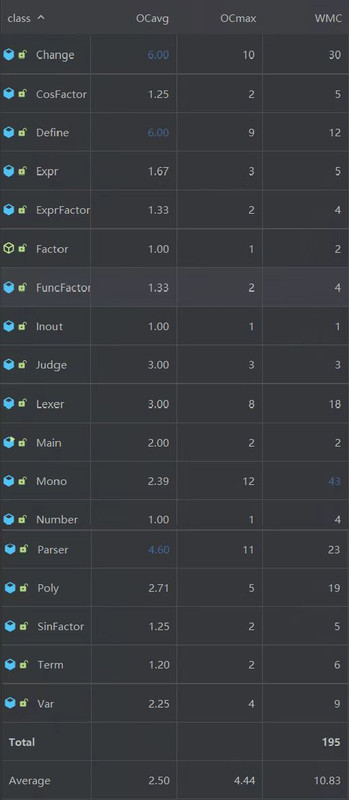
复杂度分析

hw2复杂度

hw3

架构设计体验

相比第二次作业增加了求导因子

新增部分如下：

求导因子类DeFactor

以下是这个类中比较重要的数据和方法

Char ch

Expr expr

Poly toPoly(){

return expr.toDiffPoly（ch）

}
对Expr，Term和Factor（除了DeFactor）增加了toDiffPoly进行求导

相比第二次作业还增加了可以在定义函数部分调用已经定义过的函数

因此新增的处理是在Define类读入定义的时候预先对表达式进行处理替换。

bug分析

这次作业在互测中被找出来了一个bug。

在前几次作业中，exprFactor的幂次不能超过8。

在这次作业中，形如

1

d(x) = (（x）**2)**6

d(x)

的数据中，由于我对d(x)定义中右边的式子在读入的时候进行了parser-toPoly-toString的处理以应对增加的“可以调用已经定义的函数”要求，所以实际上可能会遇到**(x)**12**这样的情况，原先在parseExprFactor时只读入一位幂次方的方法就会出错。

这次bug让我体会到，一种改动可能会引起蝴蝶效应产生意想不到的bug，还是应该充分测试。另一方面，如果我从第一次作业就预先按照可能会有多位来处理parseExprFactor，这样的bug也就不会产生了。

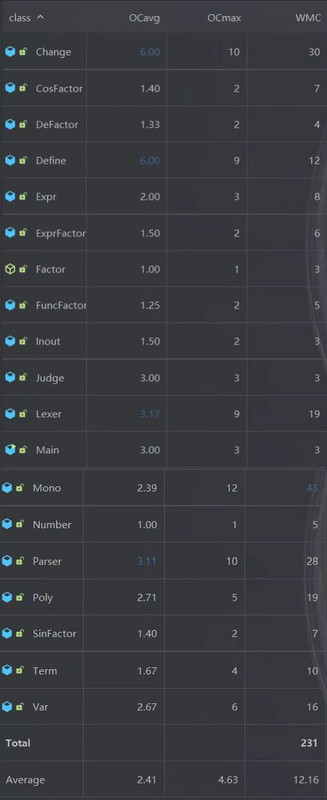
复杂度分析

hw3复杂度

心得体会

第一单元的OO作业对我来说是一个慢慢成长的过程，我看着代码风格分慢慢从不足50成长到最后一次作业的100，第一周一边学java语法一边学习面向对象知识直到ddl也完成不了任务没有通过公测，第二周在周五通过公测但是没有好好做测试没进互测，到第三周在周五通过公测并且在周日第一次进入互测。这个成长的过程是痛苦的，但是也有很多的成就感。除了对面向对象内容的学习，我还学会了很多自主学习的方法，在心态上也有非常多的成长。

查看评论